Small Proofs from Congruence Closure

Abstract

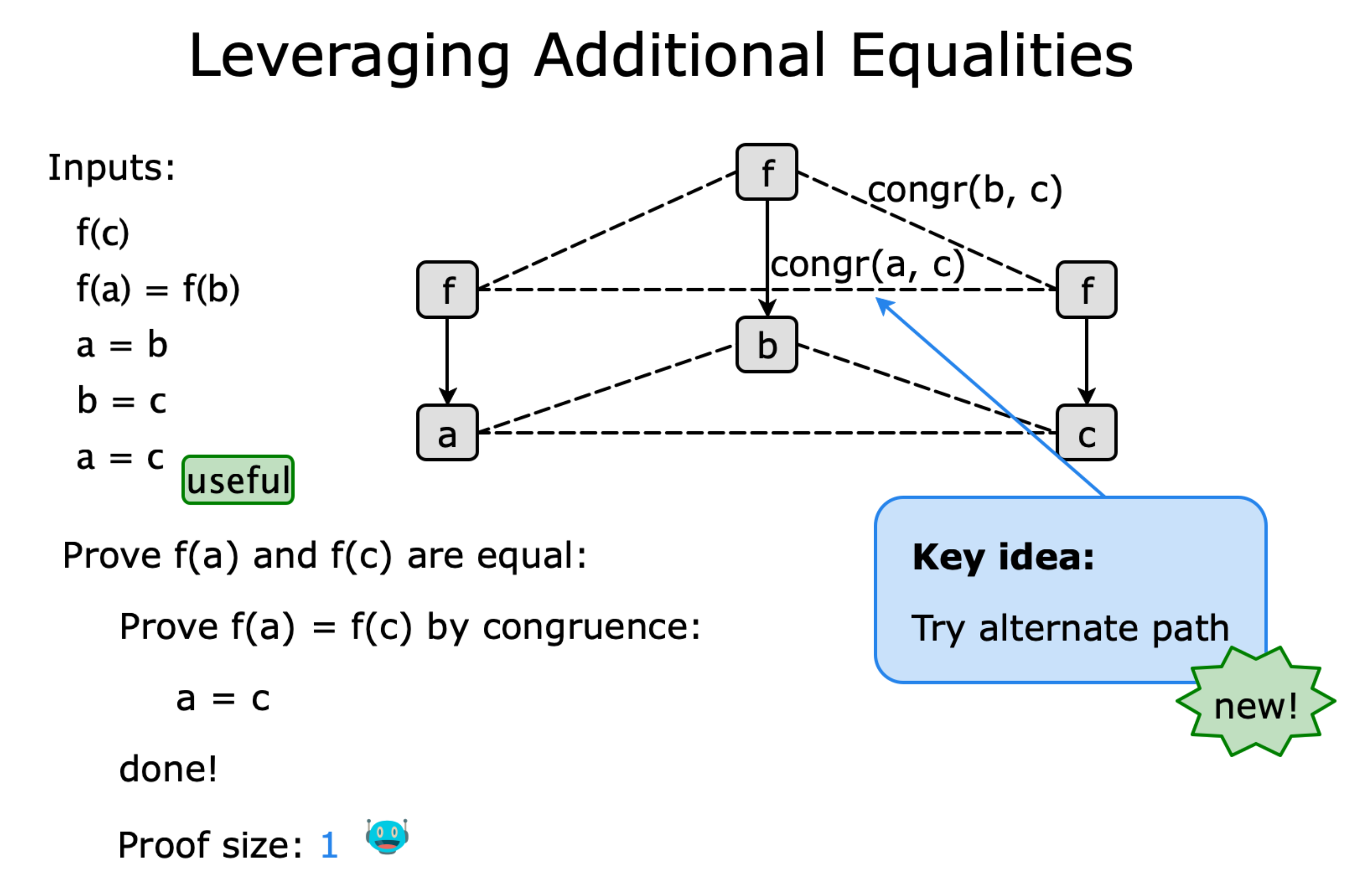
Satisfiability Modulo Theory (SMT) solvers and equality saturation engines must generate proof certificates from e-graph-based congruence closure procedures to enable verification and conflict clause generation. Smaller proof certificates speed up these activities. Though the problem of generating proofs of minimal size is known to be NP-complete, existing proof minimization algorithms for congruence closure generate unnecessarily large proofs and introduce asymptotic overhead over the core congruence closure procedure. In this paper, we introduce an O(n⁵) time algorithm which generates optimal proofs under a new relaxed “proof tree size” metric that directly bounds proof size. We then relax this approach further to a practical O(n log(n)) greedy algorithm which generates small proofs with no asymptotic overhead. We implemented our techniques in the egg equality saturation toolkit, yielding the first certifying equality saturation engine. We show that our greedy approach in egg quickly generates substantially smaller proofs than the state-of-the-art Z3 SMT solver on a corpus of 3760 benchmarks.

Talk

FMCAD 2022 talk by Oliver Flatt.

BibTeX

@inproceedings{2022-fmcad-smallproofs,
  author    = {Oliver Flatt and Samuel Coward and Max Willsey and Zachary Tatlock and Pavel Panchekha},
  booktitle = {Formal Methods in Computer-Aided Design (FMCAD) 2022},
  title     = {Small Proofs from Congruence Closure},
  year      = {2022},
  url       = {https://doi.org/20.500.12708/81325},
  doi       = {20.500.12708/81325},
}

📝 publications index